Cost Function (function that tries to fit our training set)

h(x) = Q0 + Q1x

Q0 and Q1 are parameters

How do we come up with Q1 and Q0 so that values fit in this function

lets choose Q0 and Q1 so that our (x,y) are close to this line
This is a minimization problem
sum from i = 1 to m -> h(x) - y = small so minimize this
(1/2m) * min(sum from i = 1 to m compute ---->( h(x) - y)square

So we calculate the different between 2 errors and square them. Then take the average and divide by 2. This is the cost function for linear regression

This function is also called square error cost function
This works very well for linear regression problem

Cost Function intuition:

Simplified cost function: pass through origin

h(x) = Q1x .

Q1 = 1

J(Q1) i.e J(1) = 0

Q1 = 0.5

Q1=0

Finnaly

Minimize

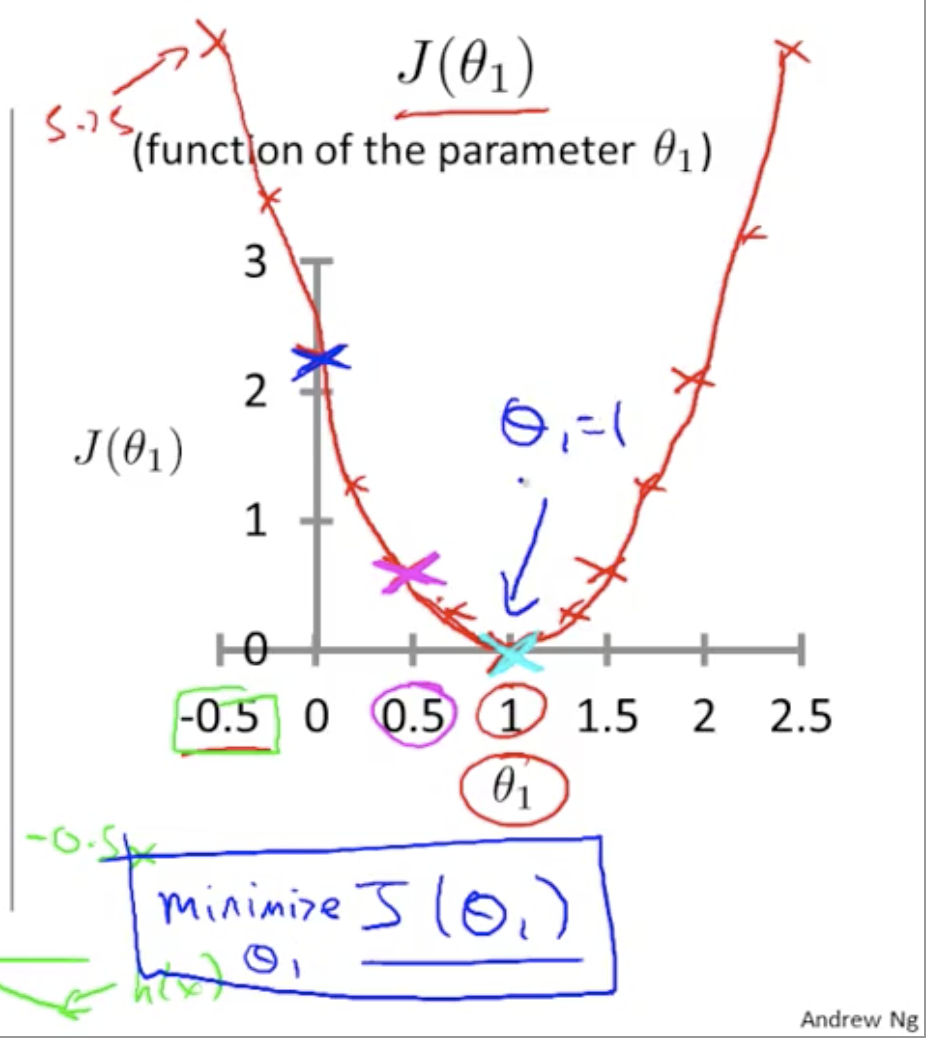
Previously when Q0=0 and we just had Q1 then the function was a parabola with minima at Q1=1. which let to straight line passing through origin

Now lets also consider Q0 . If we have both the parameters the resulting plot is also a bow shaped plot

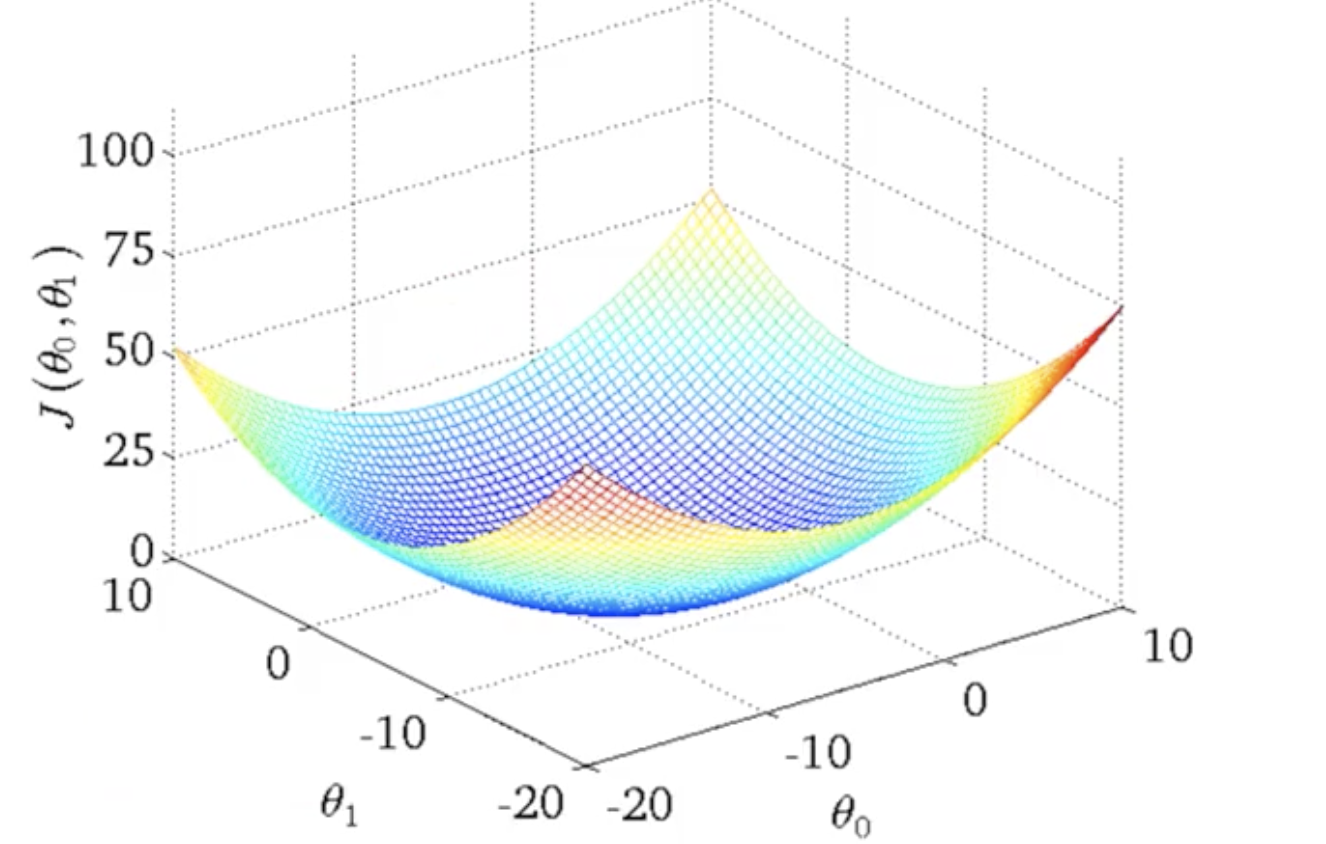
We can plot this in 2 D as contour function

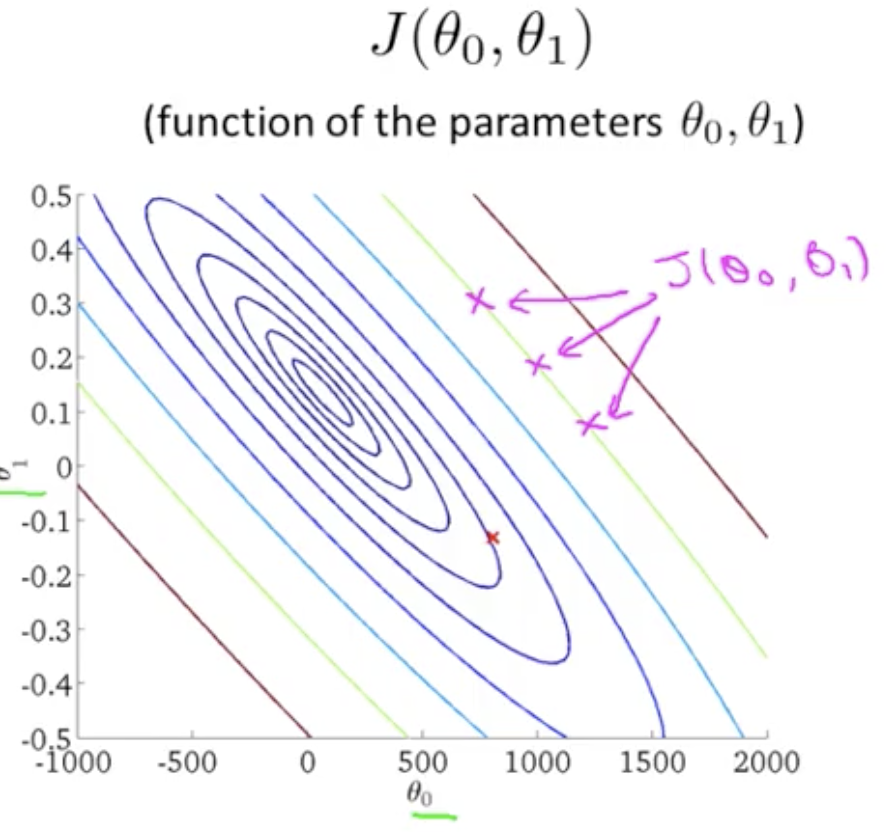
Just imagine the bow shaped 3D coming out of the screen with the base as the innermost ellipse. J(Q0,Q1) are same for points that lie on same ellipse
Now we go on seeing which h(x) will give us the minima
So we do some iterations one eg is below

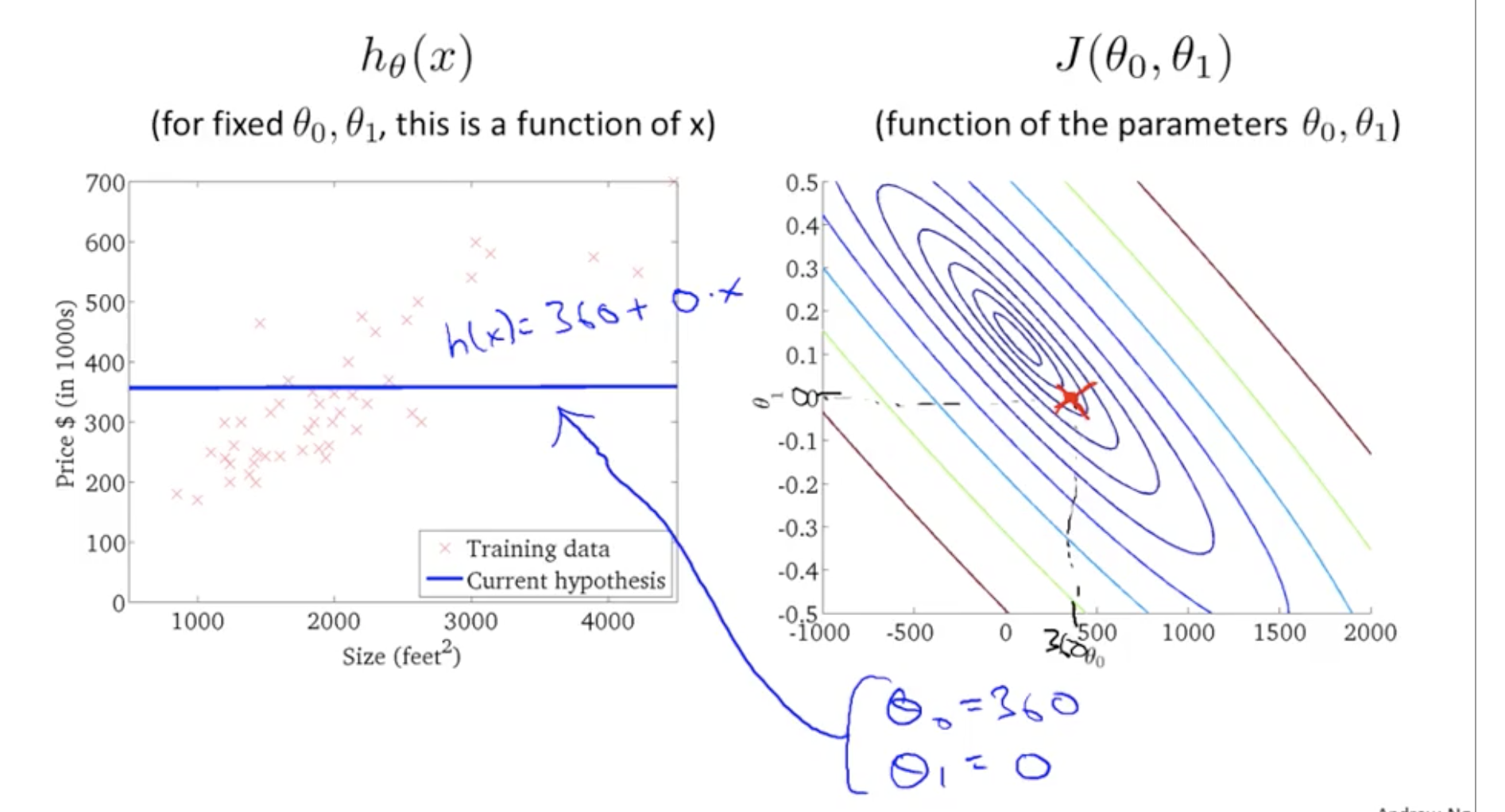
We want a efficient algorithm to find Q0 and Q1 that minimizes J

Gradient descent:

for minimizing J
keep changing Q0 and Q1 till we wind up at a local minimum
What we do in this algorithm is we spin 360 degrees take a look around and ask
- If i want to take a baby step in some direction which will minimize my value which will it be
- gradient descent depends on starting point resulting into different local optima

alpha above is called learning rate. If alpha is large its aggresive gradient descent ..big steps instead of baby
Note we must do simultaneous update as if we do otherwise we will get incorrect value

Gradient descent intuition

So basically there are 2 terms

alpha
derivative term
derivative is the tangent to the slope. So if derivative is +ve learning rate is positive Q1 = Q1- some positive number
So Q1 will move to left which is correct as slope is increading. If alpha is small we might get closer to minima
But what happens when alpha is large

Also if Q1 is at local minimum

Then it will stay there as derivative is 0.

Also as we approach local minimum no need to increase alpha as gradient descent will take smaller steps since derivative will become less steep

First learning algorithm

Result of derivatives

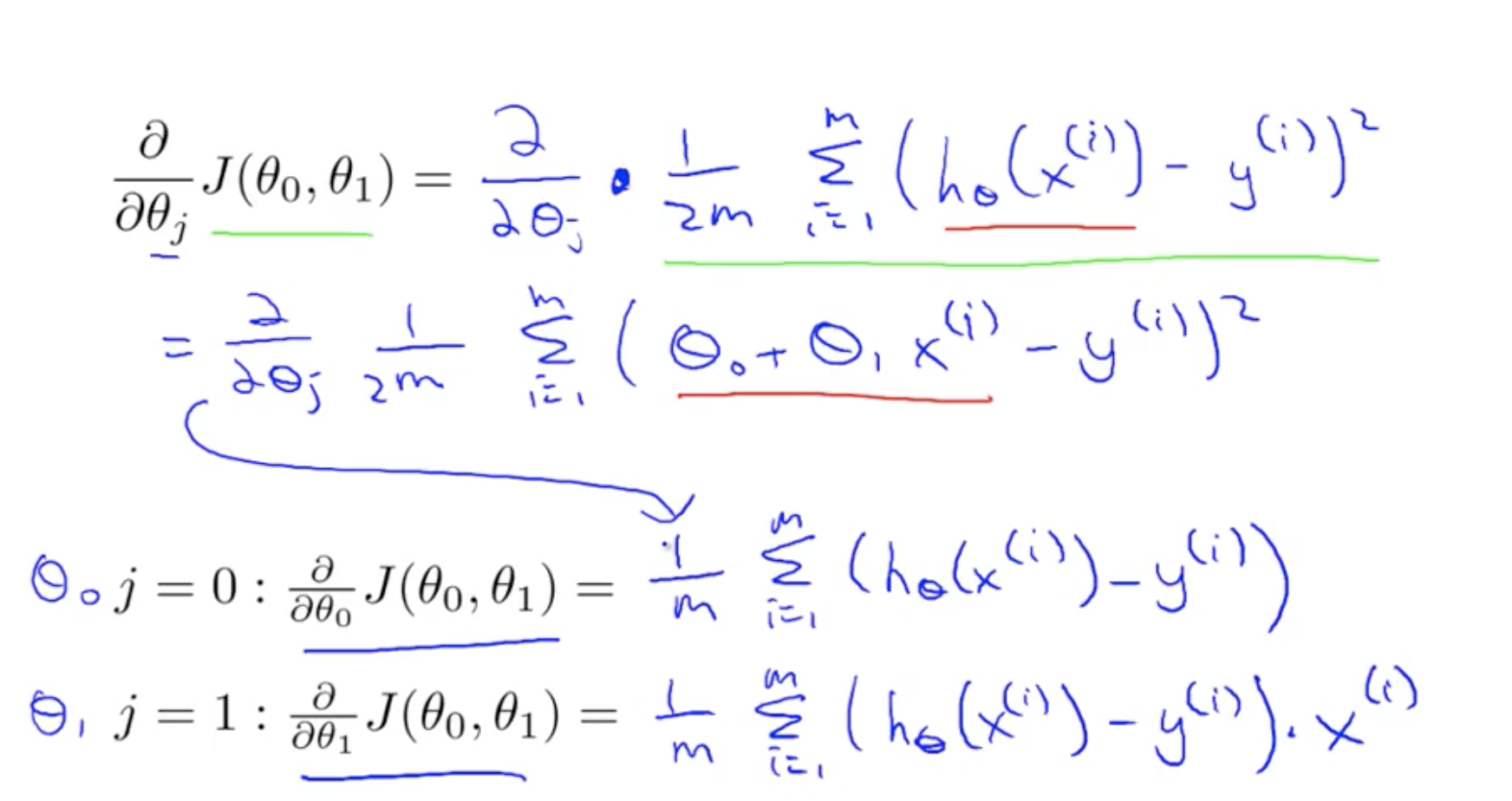
Update simultaneously

Convex function

Cost function for linear regression is always a bow shaped function and is convex (the bow shaped parabola function)
So it does not have a local optima . it only has a global optima

cost function